Robots que juegan a la biología

 Primera Parte

Las computadoras que usamos actualmente y los robots convencionales (piensen, por ejemplo, en la línea de ensamblaje de una fábrica automotriz) son consecuencia de investigaciones abstractas sobre los fundamentos de la matemática y los alcances de la lógica abstracta. La manera en que se construyen los algoritmos usuales (el conjunto de instrucciones de un robot para resolver una tarea específica) siguen las reglas matemáticas de lo que se conoce como “álgebra booleana” y funcionan siguiendo los lineamientos de una “máquina de Turing”. Cuando la ideó, Alan Turing (que aparecerá como invitado repetidas veces en esta columna y del que, por cierto, está por estrenarse una nueva película sobre su vida: The Imitation Game,), estaba interesado por una pregunta muy abstracta: ¿Podría un robot demostrar teoremas matemáticos?

Su respuesta constituye uno de los puntos de partida de la computación como la conocemos y que ya tendremos tiempo en otra ocasión de describir con detalle, pero por ahora, lo único que quiero establecer es que todas las aplicaciones con las que interactuamos cotidianamente (todos los programas, teléfonos celulares y tabletas, etc…) funcionan inspiradas por la matemática abstracta. Sin embargo, esta no es la única manera de hacer computación.

Si comparamos el funcionamiento de los robots convencionales con la forma en que los organismos biológicos resuelven las tareas específicas necesarias para su supervivencia, descubrimos que la vida, a través de la evolución, ha encontrado soluciones que superan por mucho la eficiencia de los algoritmos matemáticos abstractos.  Por ello, desde que existen las computadoras existe también un interés marcado por buscar la manera de imitar a la biología.

Para poner en su justa dimensión los avances recientes en este tipo de computación, vale la pena hacer una historia resumida de los modelos de computación que imitan a la vida. Por su extensión, este tema me tomará más de una entrega, pero estoy convencido de que la correcta aprehensión de los desarrollos más recientes que discutiré en la segunda parte, harán que este pequeño recuento histórico valga la pena.

1. Sobre las células.

La historia comienza en los primeros años de la década de los 40’s en el Laboratorio Nacional de Los Álamos. Convocados por el proyecto Manhattan, el matemático húngaro John von Newmann (otro de nuestros invitados habituales) y el matemático de origen polaco Stanislaw Ulam trabajan en conjunto y descubren que, por caminos distintos, han llegado a formular una forma de resolver problemas en común. Ulam intentaba modelar el crecimiento de cristales en un arreglo bidimensional, mientras que von Newmann se preguntaba: ¿podría un robot construir otro robot? (Claramente, una pregunta inspirada por la biología). De su colaboración nació el modelo de un “autómata celular”. Un autómata celular es un conjunto de celadas que pueden tener distintos “estados” y un conjunto de reglas sobre como evolucionan dichos estados. Podemos pensar que el conjunto de celdas está representado por una cadena de ceros y unos: 1 significa que la celda está “viva” y 0 que está “muerta”.  Por ejemplo:  11000101.

Ahora, podemos dar un conjunto de reglas sobre cómo evolucionan las celdas, en función del estado de sus vecinos, cada vez que avanzamos una unidad de tiempo,. Por ejemplo, una celda viva se queda viva si sus dos vecinos están vivos. En nuestra notación de ceros y unos, lo podríamos escribir así:

111 = 1 ;

pensando que estamos escribiendo la regla de lo que le sucede a la celda de en medio del 111. Está viva, y sus dos vecinos están vivos. Y después escribimos lo que le pasa cuando evoluciona utilizando el signo de igual: sigue viva.

010 = 0,

por ejemplo, significa que si la celda está viva, pero sus dos vecinos están muertos, entonces muere.  Así, podemos anotar las reglas para cada posibilidad.

Un caso sería:

000 = 0

001 = 0

010 = 0

011 = 0

100=  1

101 = 1

110 = 1

111 = 1

Podemos entonces empezar con un estado como el que dimos antes, y preguntarnos qué le pasa después de una evolución (estoy pensando que el primer elemento es vecino del último, como si estuvieran pegados en un cilindro. El primer renglón es el estado original, y el segundo indica cómo evolucionó):

11000101

11100010

Puedo agregar un tercer renglón, sobre cómo evoluciona después de dos unidades de tiempo, un cuarto para tres unidades de tiempo y así sucesivamente:

11000101

11100010

01110000

00111000

00011100

…

(¿notan como los tres 1 pegados se van moviendo hacia la derecha en cada paso? )

Este es un ejemplo de cómo se comporta un autómata celular binario unidimensional bajo la regla 00001111 o regla 15 (porque si escribimos 15 en binario nos da exactamente 00001111). Para autómatas celulares de una dimensión sólo existen 2⁸ = 256 posibles reglas (porque sólo hay dos estados y sólo hay ocho posibles relaciones entre estados y vecinos). Prácticamente todas se han estudiado a detalle, pero esos son sólo los autómatas celulares más sencillos. Aún quedan muchos por explorar. (En la imagen vemos la evolución de un autómata celular bajo la regla 30. En lugar de 1 y ceros, se pinta de blanco o de negro un pixel. Aquí se presentan muchísimas generaciones (renglones) y se puede ver el comportamiento complejo.

2. Sobre la vida.

Ahora bien, esta forma de hacer “evolucionar” una celda se puede extender pensando ya no en una cadena de celdas, sino en un plano bidimensional, en el que, en lugar de tener sólo dos vecinos, cada celda tiene 8 (los de los lados, los de arriba y abajo y 4 en diagonal). En 1970, en la famosa columna de Martin Gardner “Mathematical Games” de la revista Scientific American, John Horton Conway dio a conocer un conjunto de reglas de evolución para un autómata celular bidimensional que llamó simplemente “Life”, pero que hoy se conoce como “El Juego de la Vida de Conway.”

Las reglas son relativamente sencillas:

1. Cualquier celda con menos de 2 vecinos “vivos” muere

2. Si una celda viva tiene dos o tres vecinos vivos, se queda viva.

3. Cualquier celda con más de tres vecinos vivos, muere (por sobrepoblación)

4. Si una celda muerta tiene 3 vecinos vivos, en el siguiente paso estará viva, reproducción

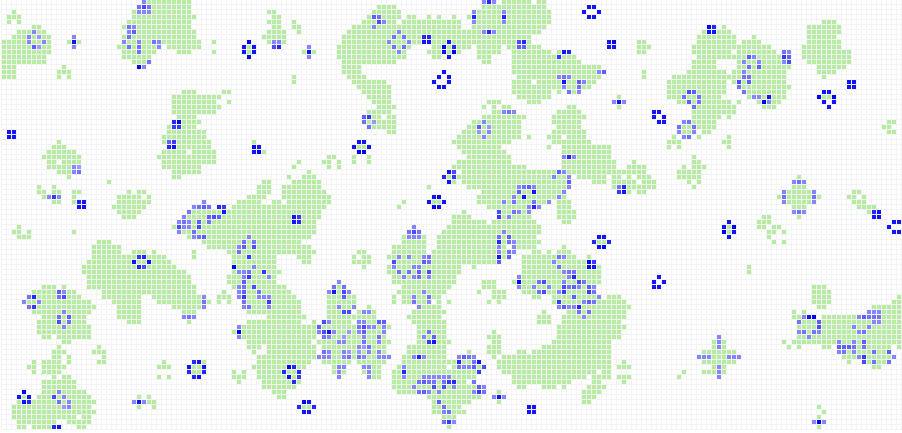
Dependiendo de la configuración inicial de arreglo bidimensional, el juego de la vida puede evolucionar en patrones muy complejos y que presentan comportamientos peculiares. Por ejemplo, es posible construir “deslizadores”: patrones que recorren el espacio sin cambiar de forma. O incluso “pistolas de deslizadores”: patrones que cuando pasa el tiempo producen “deslizadores” que a su vez recorren el espacio sin cambiar de forma. Es imposible exponer aquí todas las cosas interesantes que puede producir el juego de la vida (osciladores, “duros de matar”, emergencia, auto-replicación, etc.) por lo que  recomiendo que el amable lector se tome unos minutos para jugar por su cuenta.

En opinión de mi admirado Douglas Adams, los autómatas celulares, que constituyen la base de la computación por analogía a la evolución, han sido capaces de resolver uno de los grandes misterios de la biología: la forma en la que un conjunto muy sencillo de reglas tiene como resultado un comportamiento sumamente complejo (y, en algunos casos, caótico). Actualmente estos sistemas computacionales se usan en aplicaciones tan diversas como la simulación del tráfico en las ciudades, reacciones químicas, relaciones entre predadores y presas y, por supuesto, para estudiar la evolución.

3. Sobre la genética.

Y, hablando de evolución, la siguiente de las estrategias computacionales que imitan la vida surge del intento por copiar de un modo más realista los procesos evolutivos naturales, en particular, el mecanismo de selección natural propuesto por Darwin (y Wallace). En los autómatas celulares, la vida o muerte de una celda depende de unas reglas abstractas entre la celda y sus vecinos, y no de su desempeño en las tareas necesarias para vivir (de hecho, las celdas no realizan ninguna tarea, simplemente viven y mueren). Con esto en mente, podemos concebir un juego parecido a “Life”, pero en el que cada celda representa una forma de resolver un problema (es decir, un algoritmo).

La supervivencia del algoritmo depende de su capacidad para resolver el problema de modo más eficiente que sus vecinos. Pongamos un ejemplo concreto: imaginen que ponemos un robot en la entrada de un laberinto y queremos descubrir cuál es la mejor estrategia para encontrar la salida. Posibles estrategias son: siempre sigue la pared que tienes de tu lado izquierdo (que por cierto, es una estrategia capaz de resolver cualquier laberinto); o siempre que puedas seguir derecho sigue derecho y si no puedes, regresa a la última intersección y gira al azar y vuelve a seguir derecho (ésta no creo que resuelva un laberinto); o camina 10 pasos y luego gira a la izquierda, y luego 10 pasos y gira a la izquierda. En fin, hay muchísimas estrategias posibles. Lo que podemos hacer es poner a competir todas las que se nos ocurran y medir cuanto tiempo les toma en promedio resolver un laberinto fácil. Luego, tomamos los algoritmos que tenemos en los primeros 100 lugares y los ponemos a competir en un laberinto más complicado. Elegimos a los primeros 10 y los ponemos en un laberinto difícil. Si hacemos suficientes concursos, esperamos que el algoritmo que sobreviva al final sea el que realice la tarea de la manera más eficiente (aunque no siempre podemos asegurar que así sea). Lo que es más: si podemos dividir la tarea central en sub-tareas más sencillas, es posible que algunas estrategias sean mejores en ciertas cosas pero peores en otras, de modo que a la larga no sobreviven a pesar de tener buenas soluciones locales. ¿Por qué no imitar la vida y permitir que los algoritmos “se reproduzcan”, haciendo competir cada una de sus sub-tareas y creando una nueva estrategia que hereda lo que cada uno de sus progenitores era bueno haciendo? Esta es la idea detrás de los “algoritmos genéticos”.

Ya en 1950, Turing pensaba en una máquina capaz de aprender imitando a la evolución y durante los años 60 hubo bastante desarrollo sobre el tema, pero los algoritmos genéticos se volvieron  realmente populares por el libro de 1975 de John H. Holland, Adaptación en sistemas naturales y artificiales. Desde entonces, los algoritmos genéticos han sido utilizados para encontrar soluciones eficientes a problemas complejos en áreas como la física, química o ingeniería, así como para programar robots y comportamientos de inteligencias artificiales en video juegos.

A pesar de que la idea básica es muy clara, este tipo de computación es difícil de implementar, sobre todo porque los resultados dependen en gran medida de la forma en la que se evalúa el éxito de un algoritmo y la manera en la que se heredan las estrategias exitosas. La mayoría de las veces, definir correctamente la aptitud y la “genética” de un algoritmo puede ser un problema de igual o mayor complejidad que el problema que se pretende resolver en primera instancia. Además, las soluciones que proveen los algoritmos genéticos tienden a ser sorpresivas y oscuras, en el sentido de no es claro porque esa estrategia es eficiente o si realmente es la manera optima de resolver una tarea. En ese mismo sentido, los algoritmos genéticos se parecen a la evolución puesto que, aunque partimos de un conjunto pequeño de posible soluciones conocidas, en la medida en que las ponemos a competir encontramos mezclas cada vez más variadas y sorprendentes y por ellos son una excelente herramienta para explorar el “espacio de soluciones”.

4. Sobre las neuronas.

Sabemos que la selección natural, que en el fondo es simplemente un conjunto muy grande de pruebas tipo “acierto-error” (generado aleatoriamente), puede encontrar buenas soluciones para tareas específicas, pero que para ello necesita muchísimas generaciones, pues el número de errores siempre supera por mucho el número de aciertos. Sin embargo, conocemos un sistema biológico que, por medio del “aprendizaje”, puede modificar su funcionamiento y solucionar tareas sin necesidad de heredar información ni competir con otros: nuestro cerebro. La historia del tipo de computación que imita nuestra capacidad de aprender, conocido como “redes neuronales artificiales”, tiene antecedentes previos a los autómatas celulares (ver, por ejemplo, Warren McCulloch y Walter Pitts 1943), pero decidí dejarlo al final para favorecer la comprensión de su funcionamiento en lugar de una cronología estricta.

Partiendo de la idea del autómata celular, podemos simular el comportamiento de nuestras neuronas haciendo un par de modificaciones. Para empezar, pensemos que la conexión entre celdas vecinas puede tener cualquier valor entre 0 y 1. Es decir, los vecinos no están sólo “conectados” o “desconectados”, sino que pueden estar 30% conectados o 67.58% conectados. Las reglas básicas de “evolución” (que celdas se prenden y que celdas se apagan) de este autómata son:

1. Si una celda está prendida, contribuye a la activación de sus vecinos sólo en el porcentaje en el que está conectada.

2. Un celda apagada se activa si la suma de las contribuciones de sus vecinos es mayor que un número específico para cada celda (conocido como el “threshold” de la neurona)

Para ilustrar como se simula el aprendizaje, pongamos un ejemplo concreto. Supongan que quiero construir una red neuronal artificial que separa filas de fichas de dos colores en dos conjuntos separados que contienen sólo fichas de un color. En la notación del autómata celular podríamos decir que el problema es llevar secuencias del tipo 101010 a secuencias del tipo 000111. Construimos una red de celdas conectadas entre las que contienen la cadena que queremos separar (la forma de las conexiones, que se conoce como la “arquitectura” de la red neuronal, puede ser realmente compleja, con distintas capas de celdas y conexiones complicadas entre ellas) y las que nos da el resultado de la operación de la red.

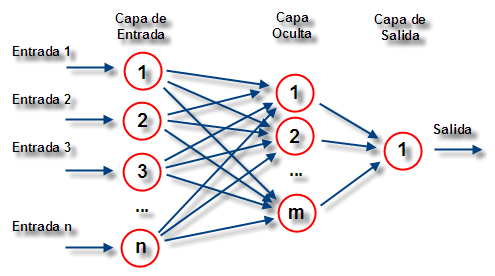
Luego, comparamos el resultado con nuestro objetivo, y si no se parecen, cambiamos un poquito el valor de las conexiones entre las celdas. Volvemos a probar que resultado arroja la operación de la red con la misma secuencia, y, sí es más parecido al objetivo, volvemos a modificar las conexiones en el mismo sentido en que lo habíamos hecho (y, si el resultado se parece “menos” al objetivo, modificamos el valor de las conexiones en el sentido opuesto). Si repetimos este proceso muchas veces, los valores de las conexiones entre vecinos se van ajustando (aprendiendo) hasta que la red neuronal logra resolver la tarea que en un principio no podía. A mí, que los robots sean capaces de “aprender” me produce ambivalencia: por un lado me maravilla, por el otro me recuerda Skynet.

Lamento que el espacio sólo me permita, por el momento, presentar estos pequeños ejemplos “de cartón”,  que si bien son excesivamente simplistas, pretenden dar, al menos, un panorama general de las estrategias computacionales que han utilizado a la biología como inspiración. En la próxima entrega discutiré tres aplicaciones muy recientes de estas ideas que, estoy seguro, resultarán más interesantes teniendo en cuenta este contexto. Como reflexión final, me queda la siguiente duda: si las computadoras fueran capaces de imitar la vida, desde las células hasta la evolución, ¿sería posible concluir que la vida “no es más” que una computadora orgánica y que la final, como decía Kraftwerk, “We are the robots”?