¿Cómo saber si nos mienten respecto a los datos del CoVid?

Hoy en día se ha convertido en parte integral de nuestra vida cotidiana: el acto de escuchar, leer y ver noticias que hablan del número de contagios, el número de muertes, cantidad de pruebas por millón de habitantes o cualquier otro tipo de información estadística que se relacione con el ya famoso virus Sars-Cov-2 y su enfermedad resultante la CoVid. Dejando un poco de lado la falta de información que en muchas situaciones nos imposibilita poner tales cifras en perspectiva y así poder extraer de ellas algún sentido, podríamos preguntarnos si los datos que nos presentan en los medios (incluso los oficiales o aquellos que asumimos como los más confiables) son correctos, o si cabe la posibilidad de que por alguna razón nos estén presentando datos que no son enteramente consistentes con la realidad, y, si este fuera el caso, ¿cómo averiguarlo?

Afortunadamente existe una forma de poder determinarlo sin tener que ser un agente encubierto. Se trata sin lugar a dudad recurrir a los estudios alternativos que nos proporciona la estadística (y de manera totalmente imparcial, a los discursos políticos respectivos a cada localidad.) Este método radica en equiparar los datos presentados en los medios o por las instituciones oficiales con la emblemática Ley de Benford, pero, ¿qué nos dice esta ley y cómo nos ayudaría a saber si las estadísticas son falaces?

Imagínense que toman una serie de números arbitraria, por ejemplo, la cantidad de habitantes de cada ciudad en un país dado, o el número de votos obtenidos por diversos candidatos en diferentes elecciones, o el precio de cualquier producto del supermercado, de hecho, puede ser casi cualquier cosa a la que se le asigna un valor numérico. Ahora miren el primer dígito de cada cifra en la lista (1 para 19, 2 para 28,568, 3 para el 372, etc.), lo que nos dice la Ley de Benford es que hay una probabilidad más alta de que el dígito con el que inicia la cifra sea el uno, es decir que en la serie se espera haya una mayor parte de cifras comiencen en uno, seguidas por las del dos, luego las del tres y así́ sucesivamente.

Este hecho puede sonar un poco contraintuitivo, pues si tenemos nueve cifras, lo más natural sería pensar que nos encontraríamos con una distribución homogénea, es decir, que en nuestra lista haya la misma cantidad de unos que de ochos o de cincos, pero no sucede así. De hecho, se presenta un fenómeno curioso, y es que la probabilidad es descendente conforme la cifra aumenta. El modelo que describe dicho fenómeno recibe el nombre de Ley de Benford y podemos observarla en la siguiente gráfica:

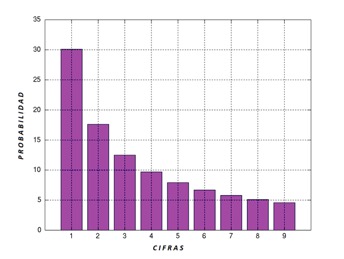
Este principio de estadística fue observado y descrito por primera vez por el astrónomo y matemático Simon Newcomb en 1881. De hecho, lo que le ayudó a descubrir esta ley poco intuitiva, fue que, al estar revisando un libro de tablas logarítmicas, se dio cuenta de que las primeras páginas estaban más gastadas que las demás, es decir, las primeras páginas eran las que más se consultaban. Cabe señalar que estos libros de tablas ordenaban los números de tal manera que al principio incluían aquellos que comenzaban en uno, posteriormente los que comenzaban en dos y así́ sucesivamente.

La observación llevó a Newcomb a preguntarse si era posible que los números que empiezan por uno, luego por dos, luego por tres, eran más utilizados que los demás. Para corroborarlo, el astrónomo examinó miles de datos de diversos orígenes y no solo confirmó que, efectivamente, seguían ese patrón, sino incluso desarrolló una fórmula que calcula la probabilidad —dada una serie de números cualquiera— de encontrar cada cifra como primera cifra significativa (la primera cifra significativa es el primer dígito distinto de 0 que aparece en la posición más a la izquierda de un número, 6 para .006856, 1 para 1763745, 3 para 3845, etc.) Según esta fórmula, la probabilidad de tener uno como primera cifra significativa es del 30.1%, tener 2 es del 17.6%, etc.

Más adelante, en 1938, y sin saber acerca de los trabajos de Newcomb, el físico Frank Benford, llegó a la misma observación y publicó sus resultados en un artículo al que llamó ‘La ley de los números anormales’ y es por eso que ahora la ley lleva su nombre. A partir de ese momento, el fenómeno empezó a ser objeto de atención de la comunidad matemática y se ha empleado para todo tipo de aplicaciones prácticas: predicciones vulcanológicas, auditorias fiscales, estadísticas deportivas, verificación de Deep fakes, entre muchos más.

Un ejemplo es que los datos de una curva con crecimiento exponencial, como son los de la epidemia que actualmente recorre el planeta, en general tienen una primera cifra significativa concordante con dicho modelo.

Dado que parece ser que la Ley de Benford puede ser aplicada a una gran parte de datos provenientes del entorno (incluso de las observaciones astronómicas), las personas familiarizadas con este fenómeno (versadas en matemáticas, estadística o actuaría) se empezaron a preguntar si de alguna manera podría utilizarse para detectar anomalías en los conteos, pues es bastante natural pensar que si algunos datos se alejan de aquellos que se esperarían de acuerdo con las distribuciones establecidas por dicha la ley, entonces lo más sensato es sospechar que hay algo raro con tales datos.

Efectivamente, en la actualidad la Ley de Benford funge como una herramienta valiosa para detectar posibles anomalías en ciertos datos, que pueden ir desde fraudes electorales hasta fiscales o estadísticas poblacionales cuestionables.

Estudios recientes en diferentes países se han llevado a cabo para encontrar posibles manipulaciones en los datos respecto a la CoVid. El “Harbert College of business” de la universidad de Auburn, en Estados Unidos, mostró que los datos proporcionados por Japón respecto al crecimiento de la CoVid en dicho país no satisfacen la Ley de Benford y por tanto son incorrectos.

Por otro lado, Christoffer Koch, economista de la Federal Research Bank de Dallas y Ken Okamura investigador de la Said Business School de la Université d’Oxford publicaron recientemente un artículo donde muestran que los datos proporcionados por China, bajo dicha prerrogativa de la Ley de Benford, parecen ser correctos.

Finalmente, Jean-François Coeurjolly de la Universidad de Quebec en Montreal analiza los datos proporcionados por Canadá, Estados Unidos y Francia, donde al parecer tampoco hay señales de manipulación.

Siguiendo estos trabajos habrá que pedirles a los matemáticos de nuestro país que verifiquen si los datos oficiales proporcionados por nuestras autoridades son o no confiables.

Por Viridiana Pérez Márquez

Referencias:

• COVID-19, flattening the curve, and Benford’s law, KangBok Lee Sumin Han, Yeasung Jeong.
• Digit analysis for Covid-19 reported data, Jean-Fran¸cois Coeurjolly, Université du Québec à Montréal (UQAM), Canada.